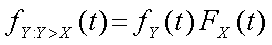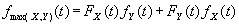
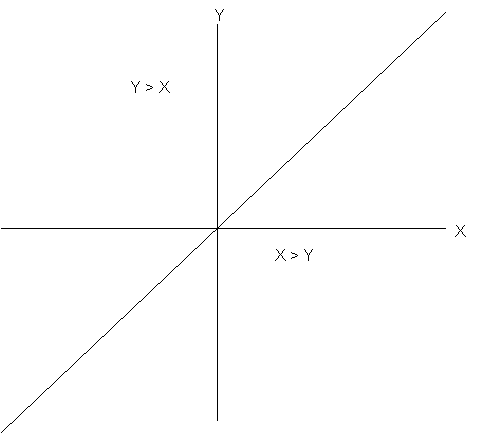
Stochasten met beslissingsmomenten

Je bepaalt de dichtheid van het maximum van twee stochasten met volgende vergelijking:


Ik ga nu op een andere wijze naar deze vergelijking kijken. Dat levert een interessante interpretatie op. In onderstaande afbeelding zijn in het platte vlak de twee stochasten X en Y weergegeven. Ook wordt de lijn Y = X getoond. Voor alle waarden onder deze lijn is X groter dan Y. Voor alle waarden boven deze lijn is Y groter dan X.
De dichtheid van het maximum is daarom een lineaire combinatie van de dichtheid van Y boven de lijn Y = X en de dichtheid van X onder die lijn. De eerste vergelijking wordt: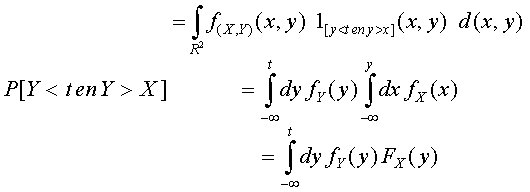


Je kunt, gebruik makend van bovenstaande formule nu de volgende dichtheidsfunctie (die ik conditionele dichtheidsfuncties zal noemen) definieren: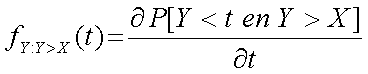


of meer algemeen: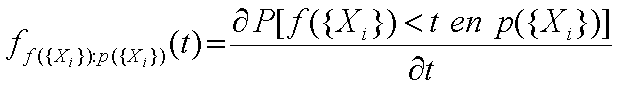



Dus     
Voor P[X > Y] geldt een analoge vergelijking. Als je de vergelijkingen samenvoegt krijg je de eerste vergelijking: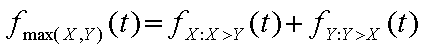
Een analoge werkwijze geldt voor het minimum. Je krijgt dan voor Y<X de volgende vergelijking: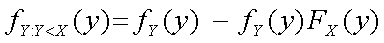

Voorbeeld 1

Stel, je wilt nu kijken naar de kans dat een stochast X groter is dan twee andere stochasten Y en Z. Daar hoort de volgende integraal bij: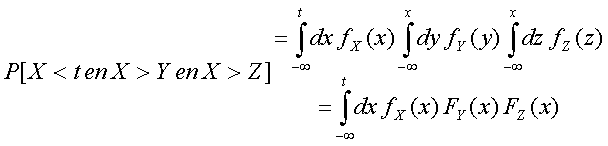


Dus

fX : X>Y en X>Z(x) = fX(x) FY(x) FZ(x)

    Analoog geldt:

  • fX : X>Y en X<Z(x) = fX(x) FY(x) (1-FZ(x))

  • fX : X<Y en X>Z(x) = fX(x) (1-FY(x)) FZ(x)

  • fX : X<Y en X<Z(x) = fX(x) (1-FY(x)) (1-FZ(x))

Voorbeeld 2

Kijk nu naar de volgende toestand: Er zijn twee stochasten X en Y. Afhankelijk van de snelste wordt een vervolgactie respectievelijk VX of VY uitgevoerd.
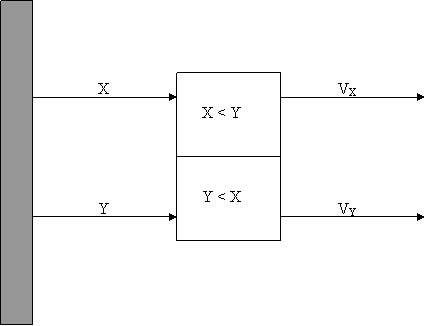
De stochast van dit proces is een lineaire combinatie van
  • (X : X<Y) + VX en
  • (Y : Y<X) + VY

ftotaal(x) = f(X:X<Y)+VX(x) + f(Y:Y<X)+VY(x)

Voorbeeld 3

In dit voorbeeld behandel ik de som van twee stochasten waarbij er een groter is dan de ander:

P[ X + Y < t en Y > X]

Kijk naar het volgend plaatje:
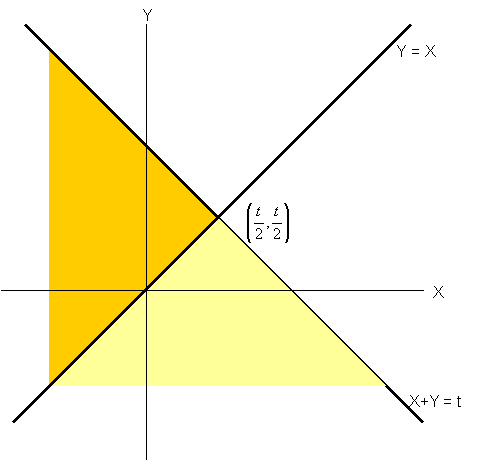
Het donkergele deel van de grafiek representeert bovenbeschreven kans. Je ziet metten de volgende zaken:
  • X < t/2
  • X < Y < t-X
Dit leidt tot de volgende integraal:
De bijbehorende dichtheid hangt op de volgende wijze van de integraal af:


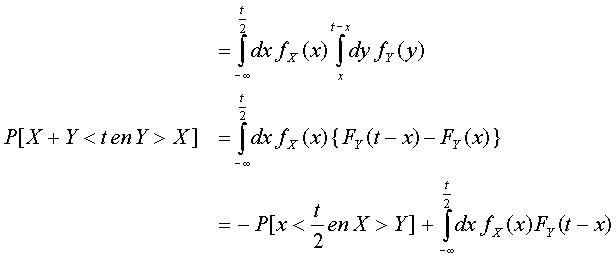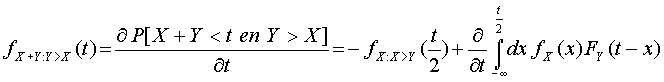
waarbij het laatste stuk nog bepaald dient te worden. Ik herdefinieer het laatste deel:


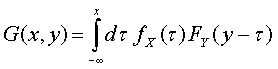
Dan kun je de afgeleide als volgt herschrijven:


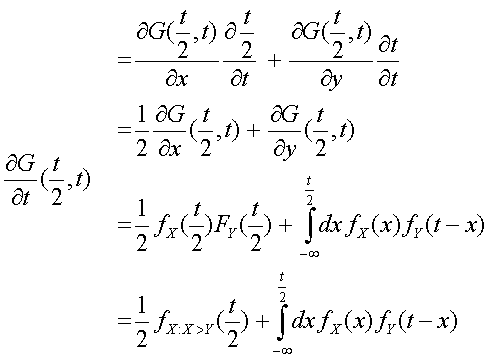
Het uiteindelijke resultaat is daarom


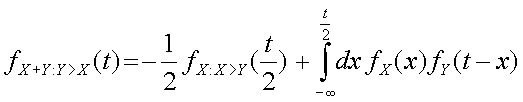
Zoals u ziet, is de laatste integraal een convolutie (een berekening behorend bij het optellen van twee stochasten) maar dan met een beperking dat de integraal loopt tot t/2.

Deze berekening zit niet in het huidige pakket. Zou je zulke berekeningen willen uitvoeren, dien je het basispakket verder uit te breiden. Dus stochasten optellen, onder voorwaarde dat ene stochast groter of kleiner is dan een andere, kan nu (nog) niet.